A misconception about microwaves
Or, “how microwaves actually work”
This is a short note on a misconception which I had and which I believe is widely shared.
As you probably know, microwave ovens are named after the type of electromagnetic radiation that they produce. Most microwaves produce radiation with a frequency of 2.45 GHz.
The misconception I had is that this frequency is tuned to one of the vibrational frequencies of the water molecule.
This is simply not true, as can be easily checked by looking up the vibration frequencies for water molecules, which are well established. The symmetric and asymmetric stretching modes have frequencies of around 108 THz and the bending mode has a frequency of 45 THz. A terahertz (THz) is 1000 faster than a gigahertz. These frequencies are in the infrared range.<figure id=”attachment_1132” class=”thumbnail wp-caption alignnone style=”width: 173px”>
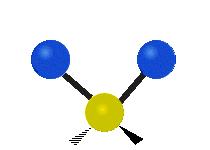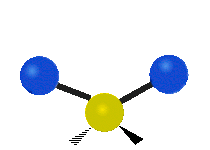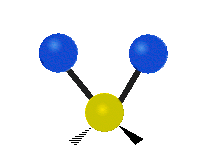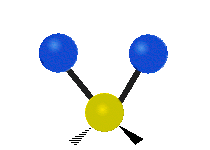<figcaption class="caption wp-caption-text">The bending mode</figcaption></figure> <figure id=”attachment_1133” class=”thumbnail wp-caption alignnone style=”width: 156px”>
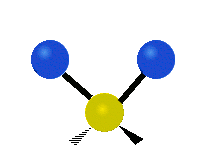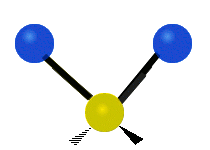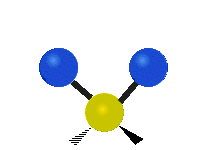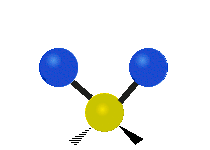<figcaption class="caption wp-caption-text">The symmetrical stretching mode</figcaption></figure> <figure id=”attachment_1131” class=”thumbnail wp-caption alignnone style=”width: 161px”>
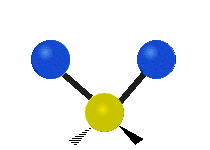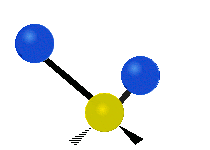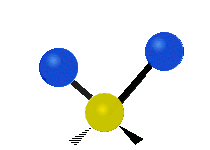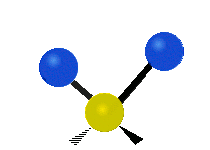<figcaption class="caption wp-caption-text">The asymmetrical stretching mode</figcaption></figure>
However, this misconception is almost true, as microwaves are tuned to one of the biggest absorption peaks of water. This is the biggest dielectric loss peak which is sometimes called the “Debye peak”.
What is the physical source of this Debye peak? The Debye peak is due to cooperative relaxations of dipoles. Water molecules process an electric dipole moment, which is simply a positive charge cloud and negative charge cloud separated by a small distance. The positive charge is on the hydrogens and the negative charge is on the oxygen. The direction of the dipole is the direction of a vector pointing from the positive to the negative charge. When an electric field is applied, a dipole feels a force which acts to cause it to rotate and point in the same direction as the field.
When an alternating electric field is applied dipoles will try to rotate with the field, as the field changes direction. At low frequencies , the dipoles have no problem keeping up with the field, but at higher frequencies frictional interactions between molecules prevent the molecule’s dipoles from keeping up and their motion lags behind the field. When this happens some of the radiation is absorbed and heat is generated. At even higher frequencies, the dipoles have absolutely no chance of keeping up, and the electromagnetic radiation passes directly through with no absorption.
Now here is the interesting part – which has to do with the name of this blog. The Debye peak is due to cooperative motions of many water molecules and is actually very complex and poorly understood. However, as I have been investigating this subject, I can give a hand-wavey explanation which captures the essential dynamics. If you were to focus on a single water molecule in the liquid you would see that it rotates pretty fast all by itself, with no field applied. Roughly speaking, this rotation is due to jiggling and bumping of the water molecule with other water molecules along with the breaking and formation of hydrogen bonds. The rate of this rotation allows us to quantify how big the frictional forces are. If we look at a water molecule’s dipole, it will have rotated by about 68 degrees after 1 ps (a ps is 10^-12 seconds) on average. This is called the dipolar relaxation time for the water molecule. After running through some equations it turns out that it is hardest to rotate water molecule’s dipoles at this rate with an electric field. This makes sense intuitively because frictional forces are causing them to rotate randomly at the same rate. This is true for individual water molecules. However, this analysis is incomplete because the electromagnetic radiation will not be acting on a single water molecule, instead, it will act on all of them, all at once. Since the water molecules themselves are all interacting, the reaction of the group will be different than the reaction of a single molecule.
If we instead consider a group of water molecules in a box about 2nm x 2nm x 2nm (corresponding to around 500 water molecules), we can consider the total dipole moment of this group. It turns out that this total dipole moment rotates much slower than the dipole moment of a single molecule — it turns 68 degrees in about 8 ps — almost 10 times slower. If we consider a bigger group, or even a macroscopic quantity with 10^23 molecules, the rotation rate remains the same. The peak in the Debye absorption occurs at this timescale. A period of 8ps corresponds to a frequency of about 12 Ghz.
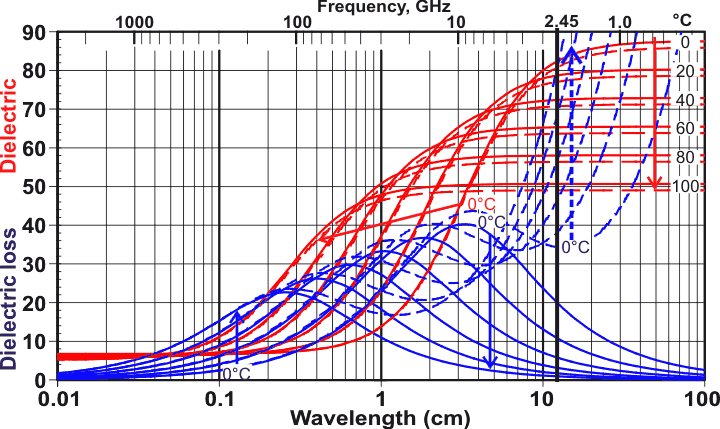
But why then, if the Debye peak is at 12 Ghz, are microwaves tuned to 2.45 GHz? The reason is that most of the water put in microwaves has stuff dissolved in it. The addition of salt, for instance, dramatically alters and shifts the Debye peak. The easiest way to see this is to look at the dielectric spectra. Check out this awesome figure, produced by Martin Chaplin and licensed under Creative Commons:
Focus on the blue curves, because they show the dielectric loss which is directly proportional to the absorption and how much heat will be generated. In the frequency range shown in this figure, all we see here is the Debye peak. It is plotted at a bunch of temperatures, ranging from 0 C to 100 C.
The dashed blue lines show the dramatic change in the shape of the loss spectrum due to the addition of salt. The vertical black line is at 2.45 GHz, which is where microwaves are tuned. Salt contains positive sodium ions and negative chloride ions which interact with water molecules in complex ways. The water molecules will form special cage structures around the ions. These cages interfere with the natural cooperative behaviour discussed before, shifting the Debye loss peak to slightly higher frequencies, and adding a lot more loss at even higher frequencies. At the same time, a new source of absorption due to the conduction of ions is added, although I believe this is mostly at lower frequencies, not shown on the graph.
It is also interesting how the loss spectrum changes with temperature. For instance, with pure water, cold water near 0C will absorb a lot less than hot water at 2.45 GHz. A ‘smart’ microwave would change the frequency as the temperature of the food changes, however this is probably very difficult to achieve.
Much more info from Martin Chaplin’s website:
Addendum
The topic of microwaves is discussed by J.B. Hasted in his obscure book Aqueous Dielectrics. I’m not recommending this as a useful book, but I include the relevant section here because it is amusing:
